The code when tested isn't proper. I've have a later more recent post on this that has tested and corrected code that should work. You can find that on my blog a few posts ahead.
Out of curiosity I did a little look up on the BiCubic re sampling method, so I found the following ordering used for supplied row coefficients. Where 16 coefficients are used in the solution process. According to the algorithm you'd need these sets of coefficients, or at least provisioning 16 points on the original 4 point grid, for example, (0,0), (1,0), (0,1), and (1,1) would be expanded to include the points (-1,-1), (-1,0), (-1, 1), (-1,2),
(0,-1), (0,0),(0,1),(0,2), (1,-1),(1,0),(1,1),(1,2), (2,-1),(2,0),(2,1),(2,2) and this leading into the computation and having handy the following:
\( H(0,0), H(1,0), H(0,1), H(1,1)\)
\( \partial H(0,0) / \partial x , \partial H(1,0) / \partial x, \partial H(0,1) / \partial x, \partial H(1,1) / \partial x \)
\( \partial H(0,0) / \partial y , \partial H(1,0) / \partial y, \partial H(0,1) / \partial y, \partial H(1,1) / \partial y \)
\( \partial^2 H(0,0) / \partial x \partial y , \partial^2 H(1,0) / \partial x \partial y, \partial^2 H(0,1) / \partial x \partial y, \partial^2 H(1,1) / \partial x \partial y \)
Of course, forward difference methods would work fine for the single partials. I searched on the mixed partials and found a central difference algorithm for this. At the moment, I hadn't thought of a method (albeit some method found typically in Image processing would suffice, I'd imagine at supplying this), that would merely encompass existing data sets without loss. Generally if you hadn't minded a little extra computation for the height map, however, you could compute say width+2 and height+2 data points and then compute differences from iterated positions 1 to size leaving all computed ("seen") points with central difference values (without conditional application for boundary conditions).
Otherwise, I found Ogre also provides in the Image class (as would any basic image library, I'd imagine) image resampling with bi cubic and bi linear filtering options. You could do this on, for instance, an image of a given height map likewise.
Here's my untested code example for generated through difference method partials.
I have to correct myself. This coefficient ordering can work when applied to computing against the 16x16 A matrix
Solve the for the alpha coefficients and the apply into the summation formula
Using, for instance the following...
(0,-1), (0,0),(0,1),(0,2), (1,-1),(1,0),(1,1),(1,2), (2,-1),(2,0),(2,1),(2,2) and this leading into the computation and having handy the following:
\( H(0,0), H(1,0), H(0,1), H(1,1)\)
\( \partial H(0,0) / \partial x , \partial H(1,0) / \partial x, \partial H(0,1) / \partial x, \partial H(1,1) / \partial x \)
\( \partial H(0,0) / \partial y , \partial H(1,0) / \partial y, \partial H(0,1) / \partial y, \partial H(1,1) / \partial y \)
\( \partial^2 H(0,0) / \partial x \partial y , \partial^2 H(1,0) / \partial x \partial y, \partial^2 H(0,1) / \partial x \partial y, \partial^2 H(1,1) / \partial x \partial y \)
Of course, forward difference methods would work fine for the single partials. I searched on the mixed partials and found a central difference algorithm for this. At the moment, I hadn't thought of a method (albeit some method found typically in Image processing would suffice, I'd imagine at supplying this), that would merely encompass existing data sets without loss. Generally if you hadn't minded a little extra computation for the height map, however, you could compute say width+2 and height+2 data points and then compute differences from iterated positions 1 to size leaving all computed ("seen") points with central difference values (without conditional application for boundary conditions).
Otherwise, I found Ogre also provides in the Image class (as would any basic image library, I'd imagine) image resampling with bi cubic and bi linear filtering options. You could do this on, for instance, an image of a given height map likewise.
Here's my untested code example for generated through difference method partials.
typedef std::pair<int, int> Coordpair;
typedef std::map<Coordpair, double> CPointsMap;
double partialx(double x, double y, CPointsMap heightmap){
//central difference (more accurate relative to forward and backwards differencing)
Coordpair * x1py = new Coordpair(x+1,y);
Coordpair * x1my = new Coordpair(x-1,y);
return (heightmap[(*x1py)] - heightmap[(*x1my)])/2.0f;
}
double partialy(double x, double y, terr::CPointsMap heightmap){
//central difference (more accurate relative to forward and backwards differencing)
Coordpair * xy1p = new Coordpair(x,y+1);
Coordpair * xy1m = new Coordpair(x,y-1);
return (heightmap[(*xy1p)] - heightmap[(*xy1m)])/2.0f;
}
double partialxy(double x, double y, CPointsMap heightmap){
//finite difference central methods
//(H(x+1,y+1)-H(x+1,y) -H(x,y+1)+2H(x,y) - H(x-1,y)-H(x,y-1)+H(x-1,y-1))/2
//or (H(x+1,y+1) -H(x+1,y-1) - H(x-1,y+1) + H(x-1,y-1))/4
Coordpair * x1py1p = new Coordpair(x+1, y+1);
Coordpair * x1py1m = new Coordpair(x+1, y-1);
Coordpair * x1my1p = new Coordpair(x-1, y+1);
Coordpair * x1my1m = new Coordpair(x-1, y-1);
return (heightmap[(*x1py1p)]-heightmap[(*x1py1m)] -heightmap[(*x1my1p)] +heightmap[(*x1my1m)])/4.0f;
}
CPointsMap BuildBicubicResample( double size, double RSize, CPointsMap heightmap){
CPointsMap * Rheightmap = new CPointsMap();
//if we want to produce from a 515 x515 grid rsize we need to have the first min at floor 1,1
//and final max at ceiling size 513,513 we need a 514 position in the central difference compute,
//so we'd need a total of 515 x 515 position in resampling a 513x513 grid.
for (int i = 1; i < RSize+1; i++){
for(int j = 1; j < RSize+1; j++){
double x = ((double) i)*(size-1.0f)/RSize +1.0f; //first row column always floored to 1 allowing central difference
double y = ((double) j)*(size-1.0f)/RSize +1.0f; //max row column always at ceiling = size
//int p0x = ((x == size ? (int)x - 1 : (int)x); int p0y = ((y == size ? (int)y - 1 : (int)y);
p0x = (int)x; p0y = (int)y;
//int p1x = ((x == size ? (int)x : (int)x + 1); int p1y = ((y == size ? (int)y : (int)y + 1);
p1x = (int)x+1; p1y = (int)y+1;
//coefficient ordering is of the following form:
// arr[0] = (H(p0x,p0y), H(p1x,p0y), H(p0x,p1y), H(p1x,p1y))
// arr[1] = (partial x H(p0x,p0y) partial x H(p1x,p0y) partial x H(p0x,p1y), partial x H(p1x,p1y))
//arr[2] = (partial y H(p0x,p0y) partial y H(p1x,p0y) partial y H(p0x,p1y), partial y H(p1x,p1y) )
//arr[3] = (mpartial xy H(p0x,p0y) mpartial xy H(p1x,p0y) mpartial xy H(p0x,p1y), mpartial xy H(p1x,p1y))
double arr[16];
Coordpair * p0xp0y = new Coordpair(p0x,p0y);
Coordpair * p1xp0y = new Coordpair(p1x,p0y);
Coordpair * p0xp1y = new Coordpair(p0x,p1y);
Coordpair * p1xp1y = new Coordpair(p1x,p1y);
arr[0] = heightmap[(*p0xp0y)]; arr[1] = heightmap[(*p1xp0y)];
arr[2] = heightmap[(*p0xp1y)]; arr[3] = heightmap[(*p1xp1y)];
arr[4] = partialx(p0x, p0y, heightmap); arr[5] = partialx(p1x, p0y, heightmap);
arr[6] = partialx(p0x, p1y, heightmap); arr[7] = partialx(p1x, p1y, heightmap);
arr[8] = partialy(p0x, p0y, heightmap); arr[9] = partialy(p1x, p0y, heightmap);
arr[10] = partialy(p0x, p1y, heightmap); arr[11] = partialy(p1x, p1y, heightmap);
arr[12] = partialxy(p0x, p0y, heightmap); arr[13] = partialxy(p1x, p0y, heightmap);
arr[14] = partialxy(p0x, p1y, heightmap); arr[15] = partialxy(p1x, p1y, heightmap);
double height = bicubicInterpolate2 (arr, x, y);
Coordpair * coord = new Coordpair(i,j);
(*Rheightmap)[(*coord)] = height;
}
}
}
I have to correct myself. This coefficient ordering can work when applied to computing against the 16x16 A matrix
Solve the for the alpha coefficients and the apply into the summation formula
double A[16][16] = {
{ 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{ 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{-3, 3, 0, 0, -2, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{ 2, -2, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{ 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0},
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0},
{ 0, 0, 0, 0, 0, 0, 0, 0, -3, 3, 0, 0, -2, -1, 0, 0},
{ 0, 0, 0, 0, 0, 0, 0, 0, 2, -2, 0, 0, 1, 1, 0, 0},
{-3, 0, 3, 0, 0, 0, 0, 0, -2, 0, -1, 0, 0, 0, 0, 0},
{ 0, 0, 0, 0, -3, 0, 3, 0, 0, 0, 0, 0, -2, 0, -1, 0},
{-9, -9, -9, 9, 6, 3, -6, -3, 6, -6, 3, -3, 4, 2, 2, 1},
{-6, 6, 6, -6, -3, -3, 3, 3, -4, 4, -2, 2, -2, -2, -1, -1},
{ 2, 0, -2, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0},
{ 0, 0, 0, 0, 2, 0, -2, 0, 0, 0, 0, 0, 1, 0, 1, 0},
{-6, 6, 6, -6, -4, -2, 4, 2, -3, 3, -3, 3, -2, -1, -2, -1},
{ 4, -4, -4, 4, 2, 2, -2, -2, 2, -2, 2, -2, 1, 1, 1, 1}}; //technically A^-12
double bicubicInterpolate2 (double[] arr, double x, double y){
double a[16];
for (int i = 0; i < 16; i++){
double sum = 0.0f;
for (int j = 0; j < 16; j++){
sum += A[i][j]*arr[j];
}
a[i] = sum;
}
double ret = 0.0f;
for (int i = 0; i<3; i++){
for (int j = 0; j<3; j++){
ret += a[i+j]*pow(x,i)*pow(y,j); //a(i,j)
}
}
return ret;
}
The method above appears to have additionally generated steps in the matrix multiplication and additions form... on the
other hand this method...
CPointsMap BuildBicubicResample2( double size, double RSize, CPointsMap heightmap){
CPointsMap * Rheightmap = new CPointsMap();
//if we want to produce from a 515 x515 grid rsize we need to have the first min at floor 1,1
//and final max at ceiling size 513,513 we need a 514 position in the central difference compute,
//so we'd need a total of 515 x 515 position in resampling a 513x513 grid.
for (int i = 1; i < RSize+1; i++){
for(int j = 1; j < RSize+1; j++){
double x = ((double) i)*(size-1.0f)/RSize +1.0f; //first row column always floored to 1 allowing central difference
double y = ((double) j)*(size-1.0f)/RSize +1.0f; //max row column always at ceiling = size
double p1x = (int)x; double p1y = (int)y;
double p2x = (int)x+1; double p2y = (int)y+1;
double p0x = p0x-1; double p0y = p0y-1;
double p3x = p1x+1; double p3y = p1y+1;
double arr[4][4];
Coordpair * p00 = new Coordpair(p0x,p0y);
Coordpair * p01 = new Coordpair(p0x,p1y);
Coordpair * p11 = new Coordpair(p1x,p1y);
Coordpair * p02 = new Coordpair(p0x,p2y);
Coordpair * p03 = new Coordpair(p0x,p3y);
Coordpair * p10 = new Coordpair(p1x,p0y);
Coordpair * p12 = new Coordpair(p1x,p2y);
Coordpair * p13 = new Coordpair(p1x,p3y);
Coordpair * p20 = new Coordpair(p2x,p0y);
Coordpair * p21 = new Coordpair(p2x,p1y);
Coordpair * p22 = new Coordpair(p2x,p2y);
Coordpair * p23 = new Coordpair(p2x,p3y);
Coordpair * p30 = new Coordpair(p3x,p0y);
Coordpair * p31 = new Coordpair(p3x,p1y);
Coordpair * p32 = new Coordpair(p3x,p2y);
Coordpair * p33 = new Coordpair(p3x,p3y);
arr = { {heightmap[(*p00)], heightmap[(*p01)], heightmap[(*p02)],
heightmap[(*p03)]},
{heightmap[(*p10)], heightmap[(*p11)], heightmap[(*p12)],
heightmap[(*p13)]},
{heightmap[(*p20)], heightmap[(*p21)], heightmap[(*p22)],
heightmap[(*p23)]},
{heightmap[(*p30)], heightmap[(*p31)], heightmap[(*p32)],
heightmap[(*p33)]}
};
double height = bicubicInterpolate (arr, x, y);
Coordpair * coord = new Coordpair(i,j);
(*Rheightmap)[(*coord)] = height;
}
}
}
Integrates both the computation of necessary derivatives, but also eliminates in the solution process zeroes that would be added steps when applied to the equation of the this form...
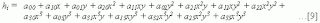
double cubicInterpolate (double p[4], double x) {
return p[1] + 0.5 * x*(p[2] - p[0] + x*(2.0*p[0] - 5.0*p[1] + 4.0*p[2] - p[3] + x*(3.0*(p[1] - p[2]) + p[3] - p[0])));
}
double bicubicInterpolate (double p[4][4], double x, double y) {
double arr[4];
arr[0] = cubicInterpolate(p[0], y);
arr[1] = cubicInterpolate(p[1], y);
arr[2] = cubicInterpolate(p[2], y);
arr[3] = cubicInterpolate(p[3], y);
return cubicInterpolate(arr, x);
}




